Polarizācija ir viena no antenu pamatīpašībām. Vispirms mums ir jāsaprot plaknes viļņu polarizācija. Pēc tam mēs varam apspriest galvenos antenu polarizācijas veidus.
lineārā polarizācija
Mēs sāksim izprast plaknes elektromagnētiskā viļņa polarizāciju.
Plakaniskam elektromagnētiskajam (EM) vilnim ir vairākas īpašības. Pirmkārt, jauda izplatās vienā virzienā (divos ortogonālos virzienos lauks nemainās). Otrkārt, elektriskais lauks un magnētiskais lauks ir perpendikulāri viens otram un ortogonāli viens otram. Elektriskie un magnētiskie lauki ir perpendikulāri plaknes viļņa izplatīšanās virzienam. Kā piemēru var minēt vienfrekvences elektrisko lauku (E lauku), kas dots ar vienādojumu (1). Elektromagnētiskais lauks izplatās +z virzienā. Elektriskais lauks ir vērsts +x virzienā. Magnētiskais lauks ir vērsts +y virzienā.
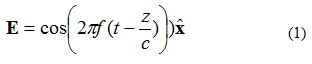
Vienādojumā (1) ievērojiet apzīmējumu: . Šis ir vienības vektors (garuma vektors), kas norāda, ka elektriskā lauka punkts atrodas x virzienā. Plakanais vilnis ir parādīts 1. attēlā.
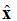
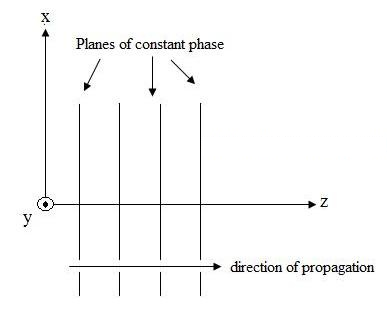
1. attēls. Elektriskā lauka, kas virzās +z virzienā, grafisks attēlojums.
Polarizācija ir elektriskā lauka pēdas un izplatīšanās forma (kontūra). Kā piemēru var minēt plaknes viļņa elektriskā lauka vienādojumu (1). Mēs novērosim pozīciju, kurā elektriskais lauks ir (X,Y,Z) = (0,0,0), kā laika funkciju. Šī lauka amplitūda ir attēlota 2. attēlā vairākos laika momentos. Lauks svārstās ar frekvenci "F".
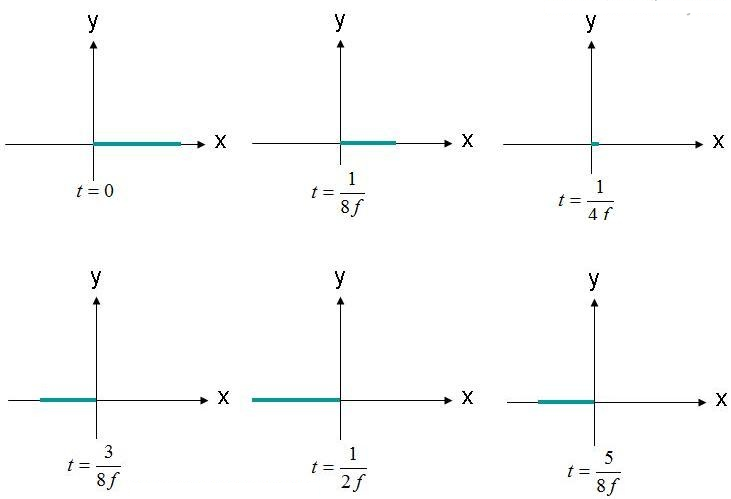
2. attēls. Novērojiet elektriskā lauka (X, Y, Z) = (0,0,0) stiprumu dažādos laikos.
Elektriskais lauks tiek novērots sākuma punktā, svārstoties uz priekšu un atpakaļ amplitūdā. Elektriskais lauks vienmēr atrodas pa norādīto x asi. Tā kā elektriskais lauks tiek uzturēts pa vienu līniju, var teikt, ka šis lauks ir lineāri polarizēts. Turklāt, ja X ass ir paralēla zemei, šo lauku var raksturot arī kā horizontāli polarizētu. Ja lauks ir orientēts pa Y asi, var teikt, ka vilnis ir vertikāli polarizēts.
Lineāri polarizētiem viļņiem nav jābūt vērstiem pa horizontālu vai vertikālu asi. Piemēram, elektriskā lauka vilnis ar ierobežojumu, kas atrodas gar līniju, kā parādīts 3. attēlā, arī būtu lineāri polarizēts.
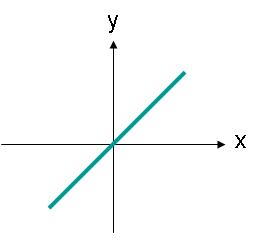
3. attēls. Lineāri polarizēta viļņa elektriskā lauka amplitūda, kura trajektorija ir leņķis.
Elektrisko lauku 3. attēlā var aprakstīt ar vienādojumu (2). Tagad elektriskajam laukam ir x un y komponentes. Abas komponentes ir vienāda lieluma.
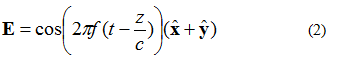
Viena lieta, kas jāņem vērā attiecībā uz (2) vienādojumu, ir xy komponente un elektroniskie lauki otrajā posmā. Tas nozīmē, ka abām komponentēm visu laiku ir vienāda amplitūda.
apļveida polarizācija
Tagad pieņemsim, ka plaknes viļņa elektrisko lauku nosaka vienādojums (3):
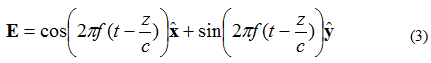
Šajā gadījumā X un Y elementi ir 90 grādu fāzes nobīdē. Ja lauku atkal novēro kā (X, Y, Z) = (0,0,0) kā iepriekš, elektriskā lauka un laika līkne izskatīsies, kā parādīts 4. attēlā.
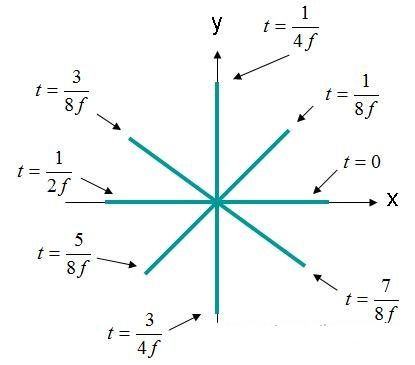
4. attēls. Elektriskā lauka stiprums (X, Y, Z) = (0,0,0) EQ apgabals. (3).
4. attēlā redzamais elektriskais lauks rotē pa apli. Šāda veida lauku raksturo kā cirkulāri polarizētu vilni. Cirkulārai polarizācijai ir jāatbilst šādiem kritērijiem:
- Apļveida polarizācijas standarts
- Elektriskajam laukam jābūt divām ortogonālām (perpendikulārām) komponentēm.
- Elektriskā lauka ortogonālajām komponentēm jābūt vienādām amplitūdām.
- Kvadratūras komponentiem jābūt 90 grādu fāzes nobīdē.
Ja pārvietojas pa 4. viļņu attēla ekrānu, lauka rotāciju sauc par pretēji pulksteņrādītāja virzienam un ar labo cirkulāro polarizāciju (RHCP). Ja lauks tiek pagriezts pulksteņrādītāja virzienā, laukam būs kreisā cirkulārā polarizācija (LHCP).
Eliptiskā polarizācija
Ja elektriskajam laukam ir divas perpendikulāras komponentes, kas atrodas 90 grādu fāzē, bet ir vienāda lieluma, lauks būs eliptiski polarizēts. Ņemot vērā plaknes viļņa elektrisko lauku, kas virzās +z virzienā, ko apraksta vienādojums (4):
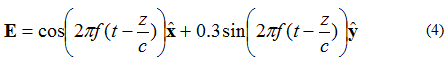
Elektriskā lauka vektora gala punkta atrašanās vieta ir parādīta 5. attēlā.
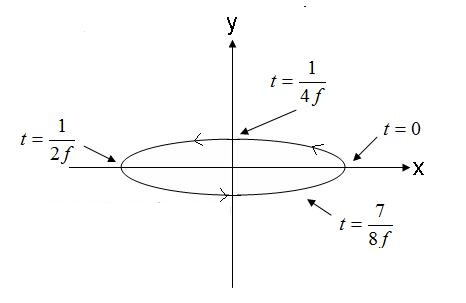
5. attēls. Ātrā eliptiskā polarizācijas viļņa elektriskais lauks. (4).
5. attēlā redzamais lauks, kas virzās pretēji pulksteņrādītāja virzienam, būtu labroči eliptisks, ja tas virzītos ārpus ekrāna. Ja elektriskā lauka vektors rotētu pretējā virzienā, lauks būtu kreisroči eliptiski polarizēts.
Turklāt eliptiskā polarizācija attiecas uz tās ekscentricitāti. Ekscentricitātes attiecība pret galvenās un blakusass amplitūdu. Piemēram, viļņa ekscentricitāte no vienādojuma (4) ir 1/0,3 = 3,33. Eliptiski polarizētus viļņus sīkāk apraksta galvenās ass virziens. Viļņu vienādojumam (4) ir ass, kas galvenokārt sastāv no x ass. Ņemiet vērā, ka galvenā ass var atrasties jebkurā plaknes leņķī. Leņķis nav nepieciešams, lai atbilstu X, Y vai Z asij. Visbeidzot, ir svarīgi atzīmēt, ka gan apļveida, gan lineārā polarizācija ir eliptiskas polarizācijas īpaši gadījumi. 1,0 ekscentrisks eliptiski polarizēts vilnis ir apļveida polarizēts vilnis. Eliptiski polarizēti viļņi ar bezgalīgu ekscentricitāti. Lineāri polarizēti viļņi.
Antenas polarizācija
Tagad, kad mēs zinām par polarizētiem plaknes viļņu elektromagnētiskajiem laukiem, antenas polarizācija ir vienkārši definēta.
Antenas polarizācija. Antenas tālā lauka novērtējums, iegūtā izstarotā lauka polarizācija. Tāpēc antenas bieži tiek uzskatītas par "lineāri polarizētām" vai "labi apļveida polarizētām antenām".
Šis vienkāršais jēdziens ir svarīgs antenu sakariem. Pirmkārt, horizontāli polarizēta antena nesazināsies ar vertikāli polarizētu antenu. Savstarpīguma teorēmas dēļ antena pārraida un uztver tieši tādā pašā veidā. Tāpēc vertikāli polarizētas antenas pārraida un uztver vertikāli polarizētus laukus. Tāpēc, ja mēģināsiet pārraidīt vertikāli polarizētu horizontāli polarizētu antenu, uztveršana nebūs iespējama.
Vispārīgā gadījumā divām lineāri polarizētām antenām, kas ir pagrieztas viena pret otru par leņķi ( ), jaudas zudumus šīs polarizācijas neatbilstības dēļ aprakstīs ar polarizācijas zudumu koeficientu (PLF):
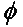
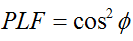
Tāpēc, ja divām antenām ir vienāda polarizācija, leņķis starp to izstarojošajiem elektronu laukiem ir nulle, un polarizācijas neatbilstības dēļ nav jaudas zudumu. Ja viena antena ir vertikāli polarizēta, bet otra - horizontāli, leņķis ir 90 grādi, un jauda netiks pārnesta.
PIEZĪME. Tālruņa pārvietošana virs galvas dažādos leņķos izskaidro, kāpēc dažreiz var uzlaboties uztveršana. Mobilo tālruņu antenas parasti ir lineāri polarizētas, tāpēc tālruņa pagriešana bieži vien var pielāgot tālruņa polarizāciju, tādējādi uzlabojot uztveršanu.
Apļveida polarizācija ir vēlama daudzu antenu īpašība. Abas antenas ir apļveida polarizētas un necieš no signāla zudumiem polarizācijas neatbilstības dēļ. GPS sistēmās izmantotās antenas ir ar labo apļveida polarizāciju.
Tagad pieņemsim, ka lineāri polarizēta antena uztver cirkulāri polarizētus viļņus. Ekvivalenti pieņemsim, ka cirkulāri polarizēta antena mēģina uztvert lineāri polarizētus viļņus. Kāds ir iegūtais polarizācijas zudumu koeficients?
Atcerieties, ka cirkulārā polarizācija patiesībā ir divi ortogonāli lineāri polarizēti viļņi, kas atrodas 90 grādu fāzē. Tāpēc lineāri polarizēta (LP) antena uztvers tikai cirkulāri polarizētā (CP) viļņa fāzes komponenti. Tāpēc LP antenas polarizācijas neatbilstības zudums būs 0,5 (-3 dB). Tas ir taisnība neatkarīgi no tā, kādā leņķī LP antena ir pagriezta. Tāpēc:
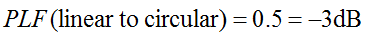
Polarizācijas zudumu koeficientu dažreiz sauc par polarizācijas efektivitāti, antenas neatbilstības koeficientu vai antenas uztveršanas koeficientu. Visi šie nosaukumi attiecas uz vienu un to pašu jēdzienu.
Publicēšanas laiks: 2023. gada 22. decembris







